こんにちわ!
ここでは高校物理や化学で使う有効数字について解説していきます!
有効数字とは
有効数字とは上から何桁まで書くかどうかということです。
例えば有効数字二桁だと
2.4とか6.2とか14とか3.0とかです。
有効数字三桁だと
2.42とか621とか14.5とか3.00とかです。
なんとなくイメージはつかめたでしょうか?
もう少し厳密に解説すると有効数字にはいくつかルールがあります。
- 小数点の位置は気にしない
523も52.3も5.32も有効数字三桁となります。
小数だろうが整数だろうが数字が何個並んでいるかどうかだけ考えます。
- 先頭に続く0はカウントしない
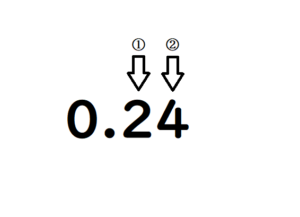
例えば0.24の有効数字は二桁です。
先頭の0はカウントしません。
また、0.0052の有効数字も二桁です。
0.00の部分はカウントせず5からカウントします。
ただし途中に出てくる0や最後の0はカウントします。
例えば1.02や5.30は有効数字三桁です。
カウントしないのは先頭に続く0だけです。
- ×10⁵ みたいなのは桁数に入れない
2.1×10⁵みたいな表し方があります。
このとき×10⁵は桁数にはカウントせず、2.1だけ見て2.1×10⁵は有効数字二桁となります。
なぜこんな書き方をするかというと2.1×10⁵ = 210000です
これだと有効数字六桁になってしまいますし、もし×10²³とかだと書くの大変過ぎますね。
練習問題
実際に何問か有効数字の問題を見てみましょう!
問題①
1.542 を有効数字二桁にしてください。
有効数字二桁なので左から3桁目を四捨五入します。
1.542 ≒ 1.542
答え 1.5
物理や化学では指定された有効数字で答えを出さなくてはいけません!
そのため答えは有効数字に合わせて四捨五入をしてください!
問題②
⅗(5分の3)を有効数字二桁にしてください。
物理や化学では分数で答えが出た場合は必ず小数にして答えます!
⅗ = 3÷5 = 0.6 = 0.60
0.6だと有効数字一桁になっているので0をつけて有効数字二桁にします
数学なら⅗のまま答えでいいんですが、物理や化学では必ず小数に直して答えなければいけないので気を付けてください!
問題③
6√2を有効数字二桁にしてください。
√(ルート)が出てきたときも必ず小数に直して答えます!
√2=1.414……≒1.41で計算します
ポイントは有効数字が二桁の場合には三桁目まで出して計算するということです!
6√2=6×√2=6×1.41=8.46=8.46=8.5〇
もし√2=1.4で計算してしまうと
6√2=6×√2=6×1.4=8.4× になってしまいます
なので指定された有効数字よりも一桁多めに出して計算します!
問題④
3249000000を有効数字二桁にしてください。
まず□×10゜みたいな形にします。
3249000000=3.249×10⁹
このとき□は1.0以上10未満になるようにしてください
32.49×10⁸や0.3249×10¹⁰にはしません(暗黙のルール)
次に有効数字二桁にするために左から3桁目を四捨五入します。
3.249×10⁹≒3.2×10⁹
答え 3.2×10⁹
有効数字が書いてない場合
物理や化学の問題集を解いていると有効数字が問題で指定されていないことも多いです。
このような場合には問題文に書かれている数値の有効数字に合わせます。
(例題)速さ5.0m/sで4.0秒進んだら何mになりますか?
5×4=20
問題文を見ると有効数字二桁で書かれています。
なので答えも有効数字二桁で答えます。
答えは20mとなります。
つい問題文の書き方につられて20.0mとしがちですがこれだと有効数字三桁になってしまうので気を付けましょう!
まとめ
・有効数字とは上から何桁まで書くかということ
・答えは指定された有効数字で答える
・分数やルートは小数に直して答える
・指定がない場合は問題文の有効数字に合わせる
いかがでしょうか?
是非参考にしてみてください!














